| 61. |
It takes 5 builders to build 5 houses in 5 days.

If the ratios remain the same, how many days should it take 100 builders to build 100 houses? |
| |
ANSWER
It should still take 5 days for 100 builders to build 100 houses if all the ratios remain the same. |
|
62. |
Three students checked into a hotel and paid the clerk $30 for a room ($10 each). When the hotel manager returned, he noticed that the clerk had incorrectly charged $30 instead of $25 for the room. The manager told the clerk to return $5 to the students. The clerk, knowing that the students would not be able to divide $5 evenly, decided to keep $2 and to give them only $3. The students were very happy because they paid only $27 for the room ($9 each). However, if they paid $27 and the clerk kept $2, that adds up to $29. What happened to the other Dollar?

|
| |
ANSWER
This is an example of adding the wrong value. The students ended up paying $27 which came from $30 - $3 = $27 and $27 + $3 is still a total of $30. The $2 the clerk kept is the additional amount the students should have also gotten back which would reduce the $27 down to the actual price of $25 (i.e. $27 - $2 = $25), the amount the students were suppose to be charged. |
|
| 63. |
The four points represent vertices of a square. How can you move exactly two points to create the vertices of a square of exactly twice the area?
|
| |
ANSWER
 |
|
| 64. |
You're on a plane to New York City. You want to know if it's snowing and the weather app on your phone doesn't always get it right. So you call 3 of your friends who live in New York City and ask each one if it's snowing. Each friend has a 2/3 chance of telling you the truth and a 1/3 chance of lying to you for fun. All 3 friends tell you, "Yes. It is snowing here." If those probabilities are accurate, what is the probability that it is in fact snowing in New York City at the moment? |
| |
ANSWERANSWER
The chance that all 3 lied is (1/3)^3 = 1/27. So, there is only a 1/27 chance that they all lied about it snowing. So the chance that just one or more of them is telling the truth is 26/27. This is a binomial probability situation of lying versus truth.
A more challenging question would be to ask what are the chances it is actually snowing if 2 friends said it was snowing and one said it wasn't. |
|
| 65. |
You have 100 pennies laying flat on a table. 10 of the pennies are heads up and 90 pennies are tails up. You are blindfolded and can't feel, see, or in any other way find out which 10 are heads up. Your goal is to split the coins into two piles so there are the same number of heads-up coins in each pile. How could you guarantee that the two piles would have the same number of heads? |
 |
| |
ANSWER
Notice, the problem didn't suggest the size of the two piles. You could take any number of coins from the pile and flip them all over to get the same number of heads in each pile.
For example....
Example#1: Let's consider taking 10 random pennies from the pile of 100. If all 10 were tails then if we flip them they would all be heads. Both piles have 10 heads.
Example#2: Let's consider again taking 10 random pennies from the pile of 100. Let's suggest that 9 were tails and 1 was heads. Then, we flip all of them.We would have 9 heads and 1 tails in the new pile and we would have 9 heads and 81 tails in the main pile. Both piles have 9 heads.
This strategy works with any size piles. Select a set number of pennies. Flip them all and we would have the same number of heads in each pile.
|
|
66. |
What is the area of the square ABCD, given only that AE = 3 units and each of the rectangles that comprise the square are equal in area?
|
| |
ANSWER
There are many ways to solve this using some visual cues, an algebraic system of non-linear equations but the only correct answer is that the square must have an area of 144 square units. If you looked at the answer before solving the brain teaser, can you prove it?
|
|
67.
|
What comes next in the following sequence?
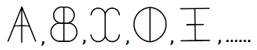
|
| |
ANSWER

|
|
|
|
|
|
|
|
|
|

